شرکت در آزمون آنلاین
هندسه 2
-
فصل دوم : تبدیل های هندسی
| آزمون شماره 65
1-
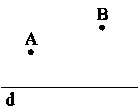
دو نقطۀ A و B به فاصلۀ افقی 6 واحد از هم و به ترتیب به فاصلۀ 3 و 5 واحد از خط d قرار دارند. طول کوتاه‌ترین مسیری که از A به B و 2 واحد روی خط d حرکت کند، چقدر است؟
2- رأس‌های A، B و C مثلث $A\mathop B\limits^\Delta C$ را به مرکز محل تلاقی میانه‌های مثلث و با نسبت $K = - \frac{1}{2}$ مجانس می‌کنیم و به ترتیب \[A'\]، \[B'\] و \[C'\] می‌نامیم. حاصل عبارت \[\frac{{A{{A'}^2} + B{{B'}^2} + C{{C'}^2}}}{{A{B^2} + A{C^2} + B{C^2}}}\] کدام است؟
3- \ \Rightarrow {I_1} = \frac{2}{3} \times \frac{1}{5} = \frac{2}{{15}}A \Rightarrow V = \frac{2}{{15}} \times 300 = 40\,(V)\]در دو دایره متداخل غیر هم‌مرکز، مرکز تجانس مستقیم و مرکز تجانس معکوس که یکی از دایره‌ها را روی دیگری تصویر می‌کند، به ترتیب کجا قرار دارند؟
4- مثلث متساوی‌الاضلاعی به ضلع 4 را یک‌بار به مرکز O و زاویة $90^\circ $ و سپس به همین مرکز و زاویة 120 دوران می‌دهیم. مساحت مثلث دوران یافته کدام است؟
5- دو شهر A و B دو طرف رودخانه هستند و می‌خواهیم جاده‌ای از A به B بسازیم به طوری که پل MN بر راستای رودخانه عمود باشد. اگر مسیر AMNB کوتاه‌ترین مسیر ممکن باشد و $A\hat MN + B\hat NM = 250^\circ $، اندازة زاویة AMK چند درجه است؟