شرکت در آزمون آنلاین هندسه 2 - فصل دوم : تبدیل های هندسی | آزمون شماره 1713

در ذوزنقه ABCD ، ضلع BC بر قاعده‌ها عمود است. اگر بدانیم طول قاعده‌های AB و CD به ترتیب برابر ۱ و ۴ و طول ساق قائم برابر ۱۰ است و نقطه M روی این ساق طوری قرار دارد که $MA + MD = t$ کمترین مقدار ممکن است ، مقدار t کدام است؟

\\begin{array}{l}{C_2}{H_4} + \cancel{{3{O_2}}} \to \cancel{{2C{O_2}}} + \cancel{{2{H_2}O}}\,\,\,\,\,\,\,\,\,\,\, - 1410\\\cancel{{2C{O_2}}} + \cancel{{3{H_2}O}} \to {C_2}{H_6} + \cancel{{\frac{7}{2}{O_2}}}\,\,\,\,\,\,\,\,\, + 1560\\\underline {{H_2} + \cancel{{\frac{1}{2}{O_2}}} \to \cancel{{{H_2}O}}\,\,\,\,\,\,\,\,\,\,} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline {\,\,\,\,\,\,\,\,\, - 286} \\{C_2}{H_4} + {H_2} \to {C_2}{H_6}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Delta H = - 136\end{array}\]در شکل زیر می‌خواهیم با استفاده از بازتاب، مساحت آن را بدون تغییر محیط افزایش دهیم. مقدار افزایش مساحت این شکل کدام مقدار زیر است؟

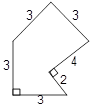
یکی از کاربردهای بازتاب، حل مسائلی است که به مسائل ......... معروف است.

درمثلث $ABC$  مجانس های مثلث را نسبت به مرکز تجانس  $C,B$  وباضریب $K>۱$  رسم میکنیم.اگر مجانس $A$  درتبدیل اول  $\acute{B}$ ومجانس $A$ درتبدیل دوم $\acute{C}$  باشد، $\acute{B} \acute{C} $ مجانس $BC$  نسبت به مرکز  $A$ ،باکدام ضریب تجانس است؟