 شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 5002
شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 5002
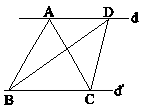
در شکل زیر دو خط d و $d'$ موازی هستند، اگر $DC = 4\sqrt 3 $ و طول ضلع AC از مثلث متساویالاضلاع ABC برابر $2\sqrt 3 $ باشد، فاصلۀ نقطۀ B تا DC چقدر است؟
در شکل زیر، AP، BQ و CR موازی هستند؛ با فرض $CR = 3$ و $AP = 5$، اندازۀ $BQ$ چقدر است؟
فرض کنید $A = {[{a_{ij}}]_{3 \times 2}}$ و ${a_{ij}} = i$، $B = {[{b_{ij}}]_{2 \times 3}}$ و ${b_{ij}} = j$ باشد، در این صورت مجموع درایههای قطر اصلی ماتریس AB کدام است؟
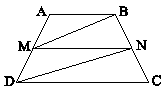
در ذوزنقة ABCD شکل زیر، MN موازی قاعدهها و MB موازی DN است. اگر $AB = 4$ و $CD = 9$ باشد؛ طول MN چقدر است؟
در مثلث قائمالزاویهی \[(\hat A = {90^ \circ })ABC\]، از نقطهی M وسط پارهخط \[AB\] بر وتر \[BC\] عمود \[MK\] را رسم میکنیم، مقدار \[K{C^2} - K{B^2}\] برابر است با:


