شرکت در آزمون آنلاین
حسابان (2)
-
فصل ١: تابع
| آزمون شماره 337
تابع f با دامنۀ $\mathbb{R}$ اکیداً صعودی است. برای $x < \alpha $، نمودار تابع $f(2x - 1)$ بالاتر از $f(3x - 4)$ است. حداکثر $\alpha $ کدام است؟
تابع f در $\mathbb{R}$ اکیداً صعودی و $f(3) = 0$ است. مجموعه‌جواب نامعادلۀ $(x + 1)f(1 - 2x) \ge 0$ کدام است؟
تابع $y = a{x^2} + 3x - 2$ در بازۀ $[ - 1\,,\, + \infty )$ یکنوا است. a کدام می‌تواند باشد؟
وارون تابع \[f(x) = 8 + {x^2}\] برای \[x \le 0\] را به کمک کدام گزینه می‌توانیم به تابع \[y = \sqrt[{}]{x}\] منطبق کنیم؟
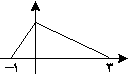
اگر نمودار $y = f(x - 2)$ شکل مقابل باشد، نمودار $y = f(2 - x)$ آن را در چند نقطه قطع می‌کند؟
