شرکت در آزمون آنلاین
ریاضی 1
-
فصل 5: تابع
| آزمون شماره 687
1- اگر $f = \{ (b\,,\,4)\,,\,( - 1\,,\,3)\,,\,(2\,,\,5)\} $، $g = \{ (4\,,\,1)\,,\,(3\,,\,7)\,,\,(2\,,\,a)\} $ و $f - g = \{ (4\,,\,d)\,,\,(c\,,\,8)\} $ باشد، حاصل $a + b + c + d$ کدام است؟
2-
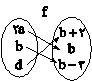
دو نمایش زیر، مربوط به تابع f هستند. حاصل $a + b + c$ کدام است؟ $f = \{ (a + 2\,,\,3)\,,\,(c\,,\,0)\,,\,(e\,,\,5)\} $
3- نمودار تابع ثابت $f$ از نقطۀ$(5\,,\,3)$می‌گذرد. اگر نمودار این تابع، نمودار تابع همانی با دامنۀ$\mathbb{R}$را در نقطۀ$A$قطع کند، مجموع مختصات نقطۀ$A$کدام است؟
4- اگر \[f = \,\left\{ {(6,1),\,( - 2,7),\,(1,\,b + 3),\,(\frac{a}{2} - 1,\,1),\,( - 3,0),\,(1,4)} \right\}\] بیانگر یک تابع باشد، مقدار\[a + b\] کدام گزینه می‌تواند باشد؟
5- کدام گزینه هرگز رخ نمی‌دهد؟