شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل سوم : توابع

1

اگر $f = \{ ( - 1\,,\,2)(0\,,\,3)(4\,,\, - 1)\} $ و $g = \{ ( - 1\,,\,b)(0\,,\,1)(2\,,\,2)\} $ باشند، شرط آنکه تابع $\frac{{2f}}{{g + 1}}$ اکیداً صعودی باشد، کدام است؟

$b \in \mathbb{R} - [ - ۱\,,\,\frac{۱}{۳}]$

$b \in (\frac{۱}{۳}\,,\, + \infty )$

$b \in ( - \frac{۱}{۳}\,,\,۱)$

$b \in ( - ۱\,,\,\frac{۱}{۳})$

2

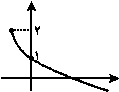
اگر نمودار تابع $y = - \sqrt {x + a} + b$ به‌صورت زير باشد، حاصل ${a^2} - b$ كدام است؟

$ - ۱$

$ - ۲$

$ - ۳$

$ - ۴$

3

اگر دامنة توابع $f(x) = \frac{{x - 1}}{{\frac{1}{{x + 2}} - 3}}$ و $g(x) = \frac{x}{{a{x^2} + bx - 2}}$ یکسان باشد، حاصل \[a + b\] کدام است؟

$\frac{{۱۴}}{۵}$

$ - \frac{{۱۴}}{۵}$

$ - \frac{{۱۱}}{۳}$

$\frac{{۱۱}}{۳}$

4

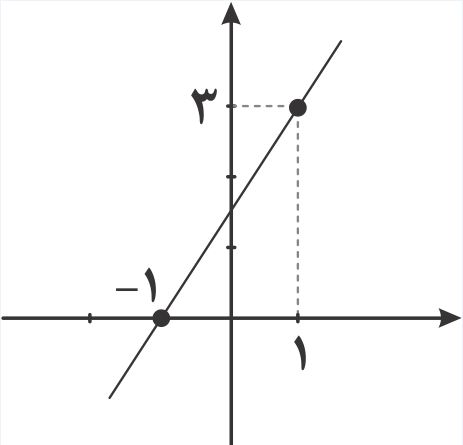
اگرنمودار تابع $f$ به صورت مقابل باشد، ضابطه ی وارون آن کدام است؟

$y=\frac{۳}{x}+\frac{۳}{۲}$

$y=\frac{۲}{۳}x-۱$

$y=\frac{-۲}{۳}x+۱$

$y=\frac{۳}{۲}x+۱$

5

اگر وارون تابع $f\left ( x \right )=ax+۳ $ برخود آن منطبق باشد، مقدار $f(a)$ کدام است؟

$۲$

$-۲$

$۴$

$-۴$

شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل سوم : توابع | آزمون شماره 122

جست و جو

شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل سوم : توابع | آزمون شماره 122

جست و جو

ساخت آزمون

ساخت آزمون