شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل ششم : حد و پیوستگی
| آزمون شماره 182
تابع $f(x) = [ - {x^2} + 2x]$ در کدام‌یک از نقاط زیر حد دارد؟ ($[\,\,]$ نماد جزء صحیح است.)
اگر تابع \[y = f(x)\] در \[x = a\] حد داشته باشد و بدانیم \[\mathop {\lim }\limits_{x \to a} \frac{{{f^2}(x) + 1}}{{f(x)}} = 2\] است، حاصل \[\mathop {\lim }\limits_{x \to (a - 1)} f(x + 1)\] کدام است؟
اختلاف حد چپ و راست تابع \[f(x) = [{x^2} - 4x + 2]\] در نقطة \[x = 2\] کدام است؟
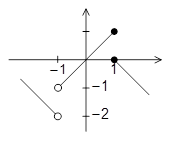
نمودار تابع \[y = f(x)\] به شکل مقابل است. اگر \[g(x) = \left\{ {\begin{array}{*{20}{c}}{f(x + 2) + a\,\,\,\,\,x \ge - 1}\\{2\,[f(x)]\,\,\,\,\,\,\,\,\,\,\,\,\,\,x < - 1}\end{array}} \right.\] در \[x = - 1\] پیوسته باشد، a کدام است؟
به ازای کدام مقدار a، تابع $f\left ( x \right )=\left\{\begin{matrix} \frac{\left | x+۱ \right |}{x+۱}\sqrt{\left | x+۱ \right |} &x\neq -۱ \\ a+۲ &x=-۱ \end{matrix}\right.$ در x=-۱ پیوسته است؟
