شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 4497
شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 4497
فرض کنید $A = {[{a_{ij}}]_{3 \times 2}}$ و ${a_{ij}} = i$، $B = {[{b_{ij}}]_{2 \times 3}}$ و ${b_{ij}} = j$ باشد، در این صورت مجموع درایههای قطر اصلی ماتریس AB کدام است؟
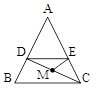
در شکل روبهرو \[DE||BC\] و M وسط DC است. اگر \[{S_{\mathop {DEM}\limits^\Delta }} = \frac{1}{4}{S_{\mathop {ADE}\limits^\Delta }}\] آنگاه مساحت ذوزنقة DECB چند برابر مساحت مثلث ADE است؟
در ذوزنقة ABCD از محل تلاقی قطرها خطی موازی قاعدهها رسم میکنیم تا ساقهای ذوزنقه را در M و N قطع کند. اگر نسبت طول قاعدهها $\frac{1}{4}$ باشد، طول MN چند برابر قاعدة بزرگ است؟
در ذوزنقة ABCD مطابق شکل، حاصل \[2z + t\] کدام است؟
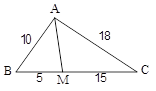
در شکل مقابل طول AM کدام است؟