شرکت در آزمون آنلاین
هندسه 1
-
فصل سوم: چند ضلعی ها
| آزمون شماره 272
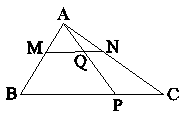
در شکل زیر، MN موازی BC و $\frac{{AM}}{{MB}} = \frac{1}{2}$ و مساحت چهار ضلعی MQPB، 24 برابر مساحت مثلث AQN است. نقطة P، ضلع BC را به چه نسبتی قطع می‌کند؟
در یک چندضلعی مجموع تعداد اقطار و تعداد اضلاع برابر 36 است. از هر رأس این چندضلعی چند قطر می‌گذرد؟
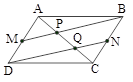
در متوازی‌الاضلاع ABCD، M و N وسط‌های AD و BC می‌باشند. اگر BM و DN، قطر AC را به‌ترتیب در P و Q قطع کنند، مساحت ABCD چند برابر مساحت مثلث PBQ می‌باشد؟
اگر تعداد قطرهای رسم شده از یک رأس n ضلعی، \[{n^2} - 8n + 5\] باشد، مجموع زوایای داخلی آن چندضلعی چند برابر (90 است؟
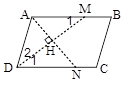
در متوازی‌الاضلاع ABCD روی ضلع AB پاره‌خط AM را مساوی AD جدا می‌کنیم. از A عمود AH را بر DM وارد می‌کنیم تا ضلع DC را در N قطع کند. اگر طول متوازی‌الاضلاع 5 و محیط AMND برابر 8 باشد، قطعة NC برابر است با:
