 شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 4567
شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 4567
1-
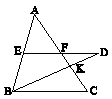
در شکل زیر، $ED||BC$ است. اگر $EF = FD$، $AF = 9$ و $CK = 6$ باشد، طول $FK$ چقدر است؟
2- در مثلث قائمالزاوية ، از نقطة N وسط ضلع AC بر وتر BC عمود ميكنيم و پاي عمود را K ميناميم و از K به وسط ضلع AB، نقطة M، وصل مينماييم. مساحت چهارضلعي ANKM چه كسري از مساحت مثلث است؟
3- روی پارهخط AB به طول 14 واحد نقاط P و Q را به گونهای انتخاب کردهایم که \[\frac{{QA}}{{PA}} = \frac{{PB}}{{QB}} = \frac{5}{2}\] است. طول PQ چقدر است؟
4-
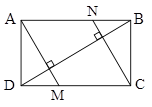
در مستطیل ABCD پارهخطهای AM و CN را طوری رسم کردهایم که بر قطر BD عمود باشند. اگر طول اضلاع مستطیل 4 و 5 واحد باشند، اندازة ضلع کوچکتر متوازیالاضلاع ANCM کدام است؟
5- در شكل زير، اگر $AC\parallel BD$ و $ED\parallel BC$ باشد و $OA = 1$ و $AB = 2$ باشد، اندازة OE كدام است؟