شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 3936
1-
در شکل زیر، چهار نقطة M، N، P و Q طوری روی یک خط قرار گرفته‌اند که $\frac{{MN}}{{NP}} = \frac{{MP}}{{PQ}} = \frac{4}{3}$، اگر $MQ = 14$ باشد، طول پاره‌خط PQ کدام است؟
2-
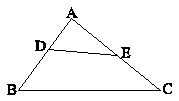
در مثلث زیر $AB = 4AD$، $EC = 3AE$ و $DE = 5$ است. اگر محیط مثلث ABC، 44 باشد، محیط مثلث ADE کدام است؟
3- در مثلث قائم‌الزاویۀ ارتفاع AH وارد بر وتر BC را رسم می‌کنیم $(CH > BH)$. اگر مساحت مثلث متوسط واسطۀ هندسی بین مساحت مثلث کوچک‌تر و مساحت مثلث باشد، کدام رابطه صحیح است؟
4- روی پاره‌خط AB به طول 14 واحد نقاط P و Q را به گونه‌ای انتخاب کرده‌ایم که \[\frac{{QA}}{{PA}} = \frac{{PB}}{{QB}} = \frac{5}{2}\] است. طول PQ چقدر است؟
5-
در مثلث قائم‌الزاویة $(A = 90^\circ )$، با رسم ارتفاع AH، نسبت مساحت‌های دو مثلث $\mathop {ABH}\limits^\Delta $ و \[\mathop {ACH}\limits^\Delta \] 1 به 4 می‌باشد. اگر $AB = 3$ باشد، طول وتر BC کدام است؟
