شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل ششم : حد و پیوستگی | آزمون شماره 358

1- اگر تابع \[f(x) = \left\{ {\begin{array}{*{20}{l}}{\mathop {\frac{{2\,[2\cos (x + \frac{\pi }{3})]}}{{2ax + a}}}\limits_{} }&{x > 0}\\{\mathop {\,\,\,\,\,\,\,\,\,\,\,\,\,b}\limits_{} }&{x = 0}\\{\frac{{{{(x + 2)}^3} + {{(x - 2)}^3}}}{{{x^4} - 4x}}}&{x < 0}\end{array}} \right.\] در نقطۀ $x = 0$ پیوسته باشد، حاصل ab کدام است؟ ($[\,\,]$ نماد جزء صحیح است.)

2- تابع $y = [\frac{{1 - 4x}}{5}]$ در چند نقطه روی فاصلة $(3\,\,,\,\,8)$ حد ندارد؟

3- اگر تابع f در نقطة \[x = a\] حد نداشته باشد، کدام یک از توابع زیر قطعاً در نقطة \[x = a\] فاقد حد است؟

4-

با توجه به نمودار مقابل حاصل $\lim_{x→۱}⁡(-f(x))+\lim_{x→۱}⁡f(-x) $ کدام است؟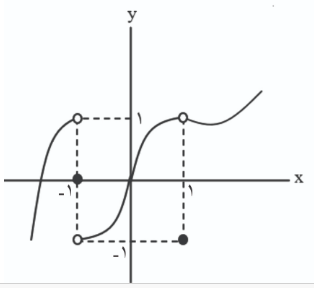 

5-

اگر حد تابع $\text{f}$ با دامنه‌ی $\mathbb{R}$ در تمام نقاط موجود باشد و داشته باشیم $\underset{\text{x}\to ۲}{\mathop{\lim }}\,\frac{۲{{\left( \text{f}\left( \text{x} \right) \right)}^{۲}}-۳\text{f}\left( \text{x} \right)}{\text{f}\left( \text{x} \right)+۱}=۴$ حاصل $\underset{\text{x}\to ۲}{\mathop{\lim }}\,۴\text{f}\left( \text{x} \right)+۱$ با کدام یک می‌تواند برابر باشد؟