شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل ششم : حد و پیوستگی | آزمون شماره 588

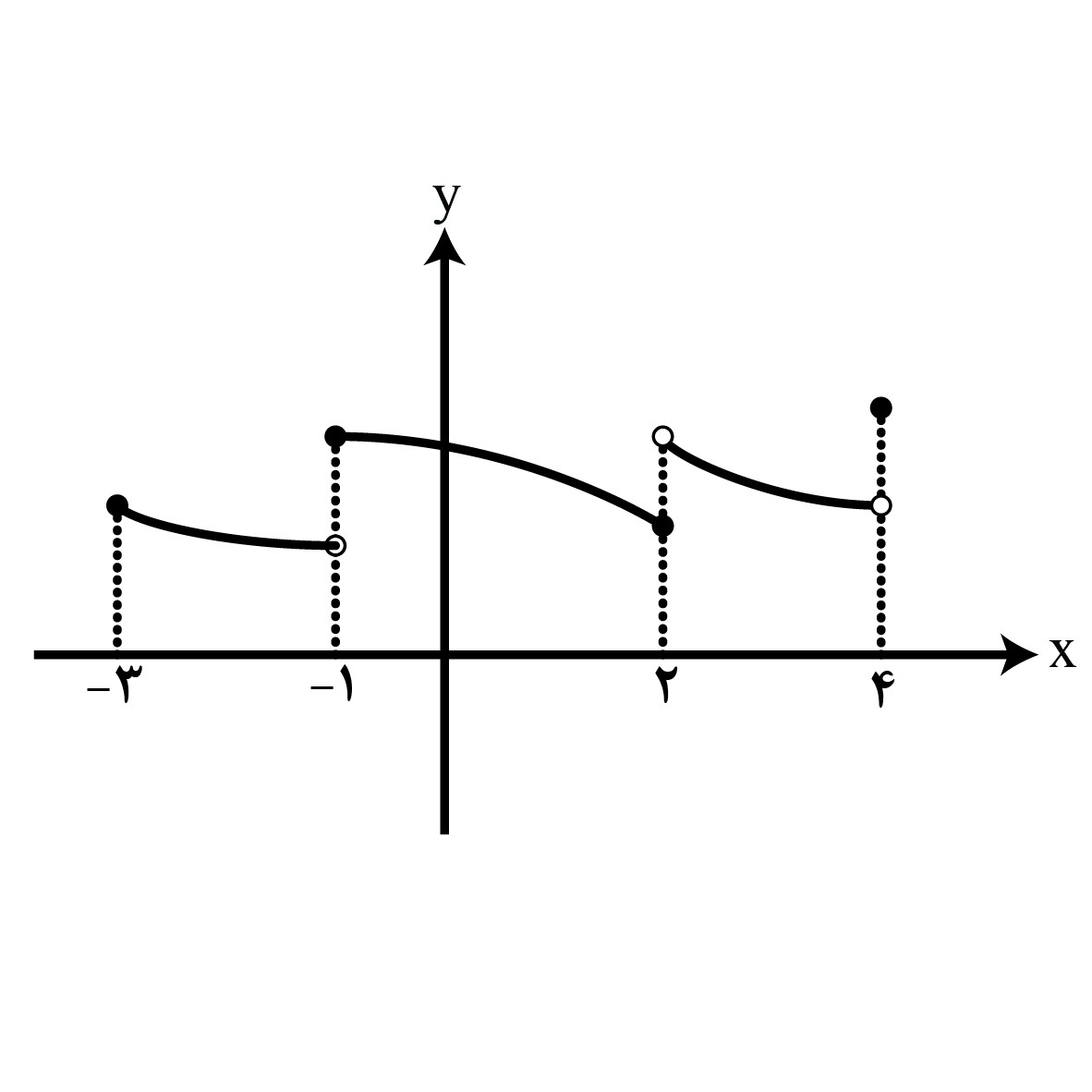
1- شکل مقابل نمودار تابع \[f(x)\] است. اگر \[g({x_0}) = f({x_0}) + \mathop {\lim }\limits_{x \to x_0^ - } f(x)\] باشد، حاصل \[g(f(3))\] کدام است؟

2- اگر تابع \[f + g\] در \[x = a\] حد داشته باشد و تابع \[f - g\] در \[x = a\] حد نداشته باشد، در این صورت کدام گزینه در مورد حد توابع f و g در \[x = a\] صحیح است؟

3- تابع پیوستۀ $f(x)$ را نسبت به محور yها قرینه کرده و سپس یک واحد بالا می‌بریم و در نهایت نسبت به محور xها قرینه می‌کنیم. اگر تابع حاصل محور طول‌ها را در $x = 2$ قطع کند، $\mathop {\lim }\limits_{x \to - 4} f(\frac{x}{2})$ چقدر است؟

4-

مقدار  $\lim\limits_{x\rightarrow (-۱)^{-}}\frac{\sqrt{x^{۲}+۲x+۱}\, \, \, \left | ۲x^{۲}-x \right |}{x+۱}$کدام است ؟

5-

نمودار تابع $f$ به صورت مقابل است. در $x=a$ رابطه $\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f\left( x \right)=f\left( a \right)$ برقرار است. $a$ کدام می‌تواند باشد؟