شرکت در آزمون آنلاین
حسابان (2)
-
فصل ٤: مشتق
| آزمون شماره 181
1- اگر f تابعی مشتق‌پذیر باشد، به طوری‌که $\mathop {\lim }\limits_{h \to 0} \frac{{f(1) - f(1 - kh)}}{h} = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{{x^2} - 1}}$ مقدار k چه عددی است؟
2- هرگاه خط \[y = 2x + 3\] بر نمودار \[y = f(x)\] در \[x = 1\] مماس باشد. مقدار مشتق \[y = xf(\frac{2}{x})\] در \[x = 2\] چقدر است؟
3- فرض کنید $f(x) = \frac{{2x + 1}}{{x + 2}}$ در نقطه‌ای با کدام طول مقادیر $f'(x)$ و $f''(x)$ با هم برابرند؟
4-
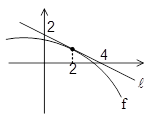
مطابق شکل مقابل خط \[\ell \] بر تابع \[f(x)\] در نقطه‌ای به طول \[x = 2\] مماس است. در این صورت شیب خط مماس بر تابع \[y = {f^2}(3x - 1)\] در \[x = 1\] کدام است؟
5-
f تابعی پیوسته است و نمودار $f'$ در مجاورت $x = \alpha $ به شکل مقابل است. نمودار f در مجاورت $x = \alpha $ چگونه است؟
