شرکت در آزمون آنلاین
هندسه 2
-
زوایای مرکزی، محاطی و ظلی
| آزمون شماره 1773
دو دایره \[C(O\,\,,\,\,2R)\] و \[C'(O'\,\,,\,\,R)\]در نقطه M مماس درون هستند. قطر MN را رسم میکنیم و از N واقع بر دایره بزرگتر، مماس NT را بر دایره کوچکتر رسم میکنیم تا امتداد آن دایره بزرگتر را در A قطع کند از M در دایره کوچکتر وتر MD را به موازات NA رسم میکنیم. مقدار MD چه ضریبی از R است؟
در شکل زیر، O مرکز دایره است و $A\hat OB = 30^\circ $. اگر ، مساحت قسمت هاشور زده برابر ${S_2}$ و $\sqrt 3 {S_1} + {S_2} = \frac{\pi }{3}$ باشند، با فرض اینکه شعاع دایره، واحد باشد، زاویۀ \[\beta \] چند درجه است؟
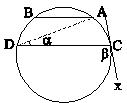
در شکل زیر، وتر AB برابر شعاع دایره و \[AB||CD\]، زاویۀ \[\beta = 4\alpha \] و CX مماس بر دایره است. کمان چند درجه است؟
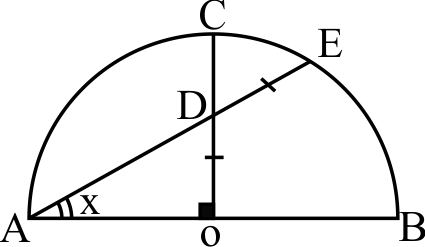
درنیم دایره شکل زیر شعاع $OC$ بر قطر$AB$عمود است و$OD=DE$ ، مقدار$X$کدام است؟
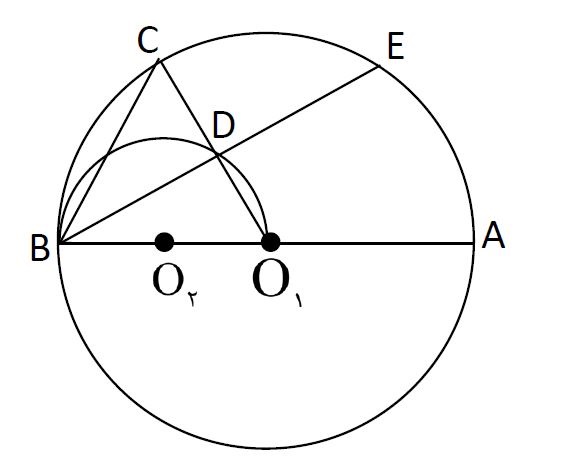
دایره به مرکز $O_۱$ بر نیمدایره به مرکز $O_۲$ در نقطۀ $B$ مماس است. اگر اندازۀ زاویۀ $O_۱\hat{C}B=۵۳°$ باشد، اندازۀ کمان $\overparen{ECB}$ کدام است؟
