شرکت در آزمون آنلاین
حسابان (2)
-
فصل ٣: حدهای نامتناهی - حد در بی نهایت
| آزمون شماره 156
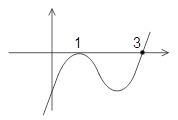
نمودار تابع $y = f(x)$ به‌صورت مقابل است. نمودار $y = \frac{x}{{f(3x + 1)}}$ در مجاورت $x = - 1$ چگونه است؟
برای تابع \[f(x) = \frac{{6x - \sqrt[{}]{{5x + 31}}}}{{a{x^n} - 2}}\] اگر داشته باشیم، \[\mathop {\lim }\limits_{x \to + \,\infty } f(x) = 3\]، حاصل \[\mathop {\lim }\limits_{x \to 1} f(x)\] کدام است؟
اگر برای تابع \[f(x) = \frac{{2\,[x] + a}}{{x - 3}}\] داشته باشیم، \[\mathop {\lim }\limits_{x \to 3} f(x) = + \,\infty \]، حاصل \[f(1)\] کدام می‌تواند باشد؟
اگر $\mathop {\lim }\limits_{x \to 1} \frac{{1 - 2x}}{{2{x^3} + ax - a - 2}} = - \,\infty $ باشد، مقدار a کدام است؟
نمودار تابع f به‌صورت مقابل است. نمودار تابع $y = \frac{{{x^2} + 1}}{{f(1 - 2x)}}$ در مجاورت $x = - 1$ چگونه است؟
