شرکت در آزمون آنلاین حسابان 1 - فصل چهارم : مثلثات

1- اگر مجموع کمترین و بیشترین مقدار تابع$f(x) = m\sin (x - \frac{\pi }{6}) + k$ برابر 6 باشد و$f(\frac{\pi }{2}) = 0$، آن‌گاه$f(\pi )$ کدام است؟

$۳ - ۲\sqrt ۳ $

$۳ + \sqrt ۳ $

$۳ - \sqrt ۳ $

$۳ + ۲\sqrt ۳ $

2- اگر $\sin (\alpha - \pi ) = \cos (\frac{{3\pi }}{2} + \beta )$ کدام گزینه می‌تواند صحیح باشد؟

$\alpha + \beta = \pi $

$\alpha + \beta = \frac{{۳\pi }}{۲}$

$\beta - \alpha = \pi $

$\alpha - \beta = \frac{\pi }{۲}$

3-

اگر $\frac{۲\tan \left (۴\alpha -۴۵^{\circ} \right )}{۱+\tan ^{۲}\left ( ۴\alpha -۴۵^{\circ} \right )}=\frac{۳}{۷}$ باشد، کدام رابطه درست است؟

$\cos ۸\alpha =\frac{۳}{۷}$

$\sin ۸\alpha =\frac{۳}{۷}$

$\cos ۸\alpha =-\frac{۳}{۷}$

$\sin ۸\alpha =-\frac{۳}{۷}$

4-

نمودار تابع $y=۱+\sin \left( x+\frac{\pi }{۶} \right)$ در بازه $\left[ ۰,k \right]$ خط $y=۲$ را در ۲ نقطه قطع می‌کند. حداقل مقدار طبیعی k کدام است؟

$۸$

$۷$

$۹$

$۱۰$

5-

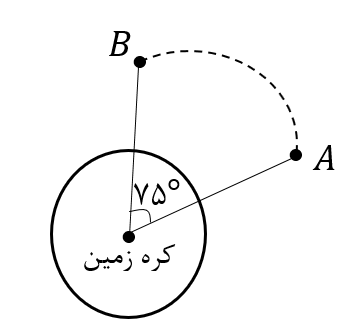
مطابق شکل ماهواره‌ای در یک مسیبر دایره‌ای در فاصله‌ی $۷۲۸$ کیلومتری از سطح زمین در حال حرکت درجهت مثلثاتی است. اگر ماهواره‌ در هر ساعت به طور متوسط مسافت $۱۲π$ کیلومتر را طی کند، چند ساعت طول می‌کشد تا از نقطه‌ی $A$ به نقطه‌ی $B$ برسد؟ (شعاع کره زمین $۶۴۰۰$ کیلومتر است)

$۲۵۰$

$۲۴۷/۵$

$۲۶۰$

$۲۵۷/۵$

شرکت در آزمون آنلاین حسابان 1 - فصل چهارم : مثلثات | آزمون شماره 643

جست و جو

شرکت در آزمون آنلاین حسابان 1 - فصل چهارم : مثلثات | آزمون شماره 643

جست و جو

ساخت آزمون

ساخت آزمون