شرکت در آزمون آنلاین
آمار و احتمال
-
درس دوم : احتمال غیر هم شانس
| آزمون شماره 1692
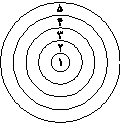
صفحۀ دارت مطابق شکل به 5 ناحیۀ مجزا تقسیم شده است. احتمال اصابت دارت به ناحیه اول برابر x و به ناحیه k ام برابر $(2k - 1)x$ است. اگر بدانیم دارت به ناحیه با شماره زوج برخورد کرده، چقدر احتمال دارد به ناحیه 2 برخورد کرده باشد؟
در یک آزمایش تصادفی، $S = \{ x\,,\,y\,,\,z\} $ فضای نمونهای است. $P(x)$، $P(y)$ و $P(z)$ تشکیل دنباله هندسی میدهند $(P(x) < P(y) < P(z))$. در صورتی که $P(x) = \frac{1}{7}$ باشد، $P(z)$ کدام است؟
4 فرد c، b، a وd در یک مسابقه شرکت کردهاند که فقط یک برنده دارد. شانس برندهشدن آنها بهصورت $P\left( a \right)=\frac{P\left( b \right)}{3}=P\left( c \right)=\frac{P\left( d \right)}{2}$ است. احتمال آنکه a یا d برنده شوند، کدام است؟
در یک تجربه تصادفی$S=\{x\,\,,\,\,y\,\,,\,\,...\,\,,\,\,z\}$ فضای نمونه است. اگر$P(z)\,\,,\,\,...\,\,,\,\,P(y)\,\,,\,\,P(x)$ یک دنباله حسابی تشکیل دهند$(P(x)<P(z))$ به طوریکه$P(x)=\frac{1}{12}$ و قدر نسبت$\frac{1}{30}$ باشد، تعداد پیشامدهای متمایزی که روی این فضای نمونه تعریف میشود کدام است؟
فضای نمونه یک آزمایش تصادفی غیرهمشانس بهصورت $S=\left\{ a,b,c,d \right\}$ است. اگر $P\left( \left\{ a,b \right\} \right)=\frac{2}{5}$ و $P\left( \left\{ a,c,d \right\} \right)=\frac{2}{3}$ باشند، آنگاه $P\left( a \right)$ برابر کدام است؟
