شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 4130
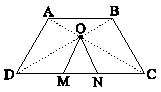
مطابق شکل زیر، از محل تلاقی قطرهای ذوزنقه، پارهخطهای OM و ON به ترتیب موازی با AD و BC رسم شدهاند. اگر $DM = 2MN = 6$، طول قاعدة CD کدام است؟
در یک مثلث قائمالزاویه، ارتفاع وارد بر وتر، مثلث مفروض را به دو جزء بهگونهای تقسیم میکند که مساحت مثلث کوچکتر $\frac{1}{{10}}$ مساحت مثلث اصلی میباشد، نسبت فاصلههای پای ارتفاع وارد بر وتر از دو ضلع قائم مثلث اصلی کدام است؟
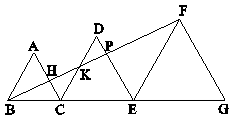
در شکل زیر، سه مثلث متساویالاضلاع به اضلاع 3، 4 و 5 در کنار هم قرار دارند. نسبت مساحت مثلث $\mathop {DKP}\limits^\Delta $ به مساحت مثلث $\mathop {PEF}\limits^\Delta $ کدام است؟
در مثلث قائمالزاویة $(A = {90^ \circ })\,\mathop {ABC}\limits^\Delta $ اگر بین اضلاع مثلث رابطة ${a^2} = 4bc$ برقرار باشد و نقطة H پای ارتفاع وارد بر وتر باشد، آنگاه حاصل $\frac{{B{H^2} + C{H^2}}}{{BH \times CH}}$ چقدر است؟
اندازة قاعدههای یک ذوزنقه 8 و 12 میباشد و O محل تلاقی دو قطر ذوزنقه میباشد. اگر فاصلة O تا قاعدة کوچکتر برابر \[\sqrt 2 \] باشد، مساحت ذوزنقه کدام است؟
