شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل دوم : هندسه

مثلث ABC با زاویة $B = 130^\circ $ و بزرگ‌ترین ضلع $6cm$ مفروض است. اگر دایره‌ای به مرکز O از هر سه رأس مثلث عبور کند، مساحت این دایره کدام می‌تواند باشد؟

$۶\pi $

$۸\pi $

$۹\pi $

$۱۰\pi $

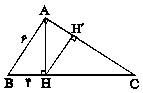
اگر در شكل زير، $AB = 6$ و $BH = 4$ باشد، طول $HH'$ كدام است؟

$\frac{{۱۰}}{۳}$

$\frac{{۱۱}}{۳}$

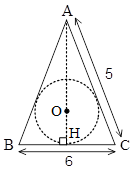
در مثلث متساوی‌الساقین ABC \[(AB = AC)\]، AH ارتفاع و O محل برخورد نیمسازهای زوایای داخلی مثلث است. در این صورت اندازة OH کدام است؟

\[{۱_/}۵\]

\[{۲_/}۵\]

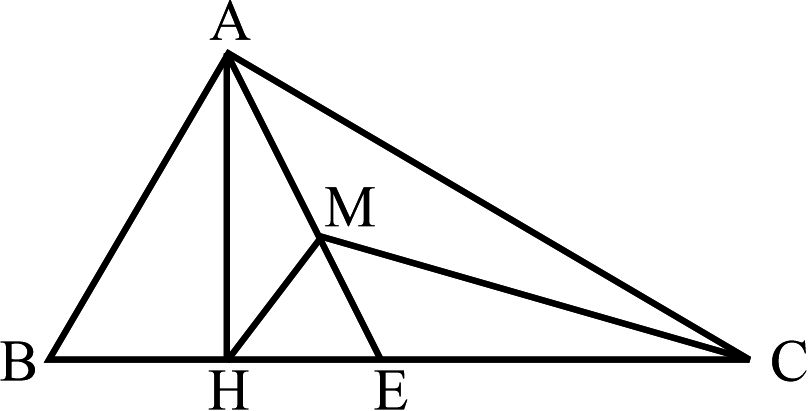
در شکل مقابل مثلث $\text{ABC}$ در رأس $\text{A}$ قائم الزاویه است $\left( \text{A}=۹۰{}^\circ \right)$ و $\text{AB}=\text{BE}$ و $\text{B}=۵۰^\circ$ و $\text{CM}$ نیمساز زاویۀ $\text{C}$ است. اگر $\text{AH}$ ارتفاع رأس $\text{A}$ باشد، اندازۀ زاویۀ $\text{MHA}$ چند درجه است؟