شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل سوم : توابع
| آزمون شماره 471
توابع $f = \{ ( - 2\,,\,4)\,,\,(0\,,\,1)\,,\,(3\,,\,7)\,,\,(8\,,\,9)\} $ و $g(x) = \sqrt {x + 1} $ مفروضند. تابع ${(f - g)^{ - 1}}$ کدام است؟
اگر دو تابع با ضابطه‌هاي $f(x) = \frac{{{x^2} - x - 6}}{{{x^2} + ax + b}}$ و $g(x) = \frac{{cx + d}}{{x - 3}}$ با هم برابر باشند، حاصل $\frac{{a + b}}{{c + d}}$ چقدر است؟
اگر تابع با ضابطة $f(x) = \left\{ \begin{array}{l}{x^2} - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x \ge 2\\ax - 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,x < 2\end{array} \right.$ معكوس‌پذير باشد، حداكثر مقدار ممكن براي a كدام است؟
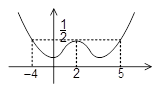
اگر نمودار \[f(x)\] به‌صورت مقابل باشد، چند عدد صحیح در دامنة \[y = \sqrt[{}]{{\frac{{^{}2f\,(\left| x \right|) - {1^{}}}}{{{{(x - 1)}^2}}}}}\] قرار ندارند؟
در کدام گزینه دو تابع f و g مساوی یکدیگر هستند؟