 شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل سوم : توابع
| آزمون شماره 446
شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل سوم : توابع
| آزمون شماره 446
اگر تابع $f(x) = \left\{ {\begin{array}{*{20}{c}}{4 - 8\sqrt x }&{x \ge 1}\\{8a - 4x}&{x < 0}\end{array}} \right.$ تابعی یک به یک باشد، حدود a کدام است؟
اگر $f\left ( x \right )=\left [ -x \right ] $ و $f\left ( a \right ) =-۴$ باشد، آنگاه حدود $a$ کدام است؟
به ازای کدام مقدار$a$ دوتابع $f=\left\{ \left ( ۳,a \right ),\left ( ۲,-۳ \right )\right\} $ و $g=\left\{\left ( k,-۳ \right ) ,\left ( ۳,k^{۲} \right )\right\}$ باهم برابراند؟
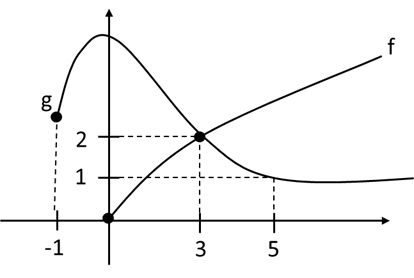
*نیازمند اصلاح در تصویر سوال: تابع g تا ۵ باید رسم شود و با دایره توپر*
اگر $f , g$ به شکل مقابل باشند، دامنه تابع $h\left( x \right)=\frac{f\left( x \right)+g\left( x \right)}{\sqrt{f\left( x \right)-۲}}$ کدام است؟
اگر دو تابع $g\left( x \right)=\left| \left| x \right|-۲ \right|,~f\left( x \right)={{x}^{۲}}-۲x-۱$ برابر باشند، دامنۀ f حداکثر چند عضو دارد؟


