شرکت در آزمون آنلاین هندسه 2 - فصل اول : دایره | آزمون شماره 1728

در مثلثی به طول اضلاع 3، 5 و 6 شعاع بزرگ‌ترین دایرۀ محاطی خارجی چند برابر شعاع کوچک‌ترین دایرۀ محاطی خارجی مثلث است؟ 

طول قاعده‌های یک ذوزنقه متساوی الساقین محیطی، ریشه‌های معادلة \[{x^2} - 8x + 4 = 0\] هستند. نسبت مساحت ذوزنقه به مساحت دایرة‌ محاطی آن کدام است؟ \[(\pi  = 3)\]

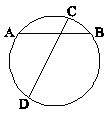
در شکل زیر، وتر CD، وتر AB را به نسبت 1 به 2 و وتر AB، وتر CD را به نسبت 1 به 4 تقسیم می‌کند. طول وتر CD چند برابر وتر AB است؟

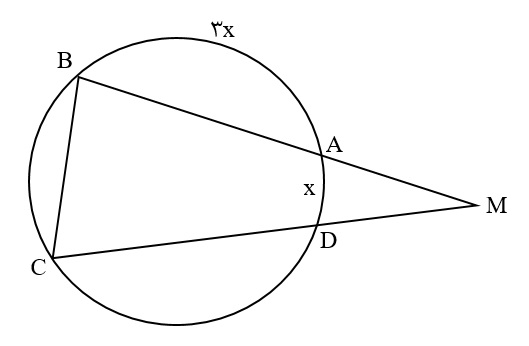
در شکل مقابل اگر $AB=BC=CD$، زاویه M چند درجه است؟

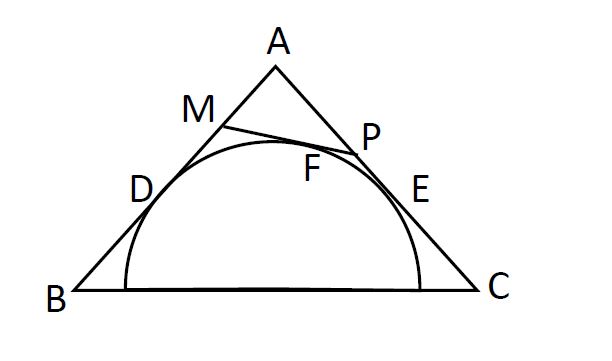
مثلث $ ABC$ به اضلاع $BC=۶$ و $AB=AC=۲\sqrt۳$ مفروض است. مطابق شکل، قطر نیم دایره ای بر ضلع $BC$ واقع است و اضلاع$ AB$ و$ AC$ و پاره خط $MP$ در نقاط $D$ ، $E$ و$ F$ بر آن مماس هستند. مقدار $BM.CP$ برابر کدام است؟