شرکت در آزمون آنلاین ریاضی 2 (رشته تجربی) - فصل دوم : هندسه

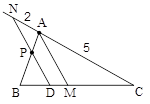
در مثلث ABC از نقطة دلخواه D روی BC خطی موازی میانة AM رسم می‌کنیم تا AB را در P و امتداد AC را در N قطع کند. با توجه به شکل، \[\frac{{AB}}{{AP}}\] چند است؟

\[{۳_/}۵\]

\[{۲_/}۵\]

در مثلث قائم‌الزاویۀ $(\hat A = 90^\circ )\,\,\mathop {ABC}\limits^\Delta $ ارتفاع وارد بر وتر،‌ مثلث اصلی را به دو مثلث کوچک‌تر تقسیم می‌کند که نسبت مساحت آنها برابر $\frac{1}{{16}}$ است. اگر اندازۀ وتر برابر $5\sqrt {17} $ باشد، مساحت مثلث $\mathop {ABC}\limits^\Delta $ کدام است؟

۱۰۰

۵۰

۸۰

۴۰

اندازه محیط‌های دو مثلث متشابه، $۱۲$ و $۱۸$ سانتی‌متر است و مساحت مثلث بزرگ‌تر، $۲۰$ واحد سطح بیشتر از مساحت مثلث کوچک‌تر است. مساحت مثلث بزرگ‌تر چند واحد است؟

$۴۵$

$۳۶$

$۴۰$

$۴۸$