شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل سوم : توابع
| آزمون شماره 534
نمودار تابع $f(x) = {\log _2}x$ را 2 واحد به سمت چپ برده و سپس آن را نسبت به محور xها قرینه می‌کنیم و در نهایت آن را 3 واحد بالا می‌بریم تا تابع $g(x)$ ساخته شود. در این صورت حاصل $g(30) + {g^{ - 1}}( - 1)$ کدام است؟
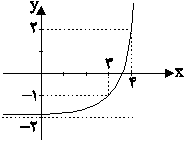
اگر نمودار تابع \[f(x) = {a^{x + b}} + c\] به صورت زیر باشد، \[{f^{ - 1}}(14)\] کدام است؟
تابع $f(x) = \left\{ {\begin{array}{*{20}{l}}{3x - k}&{x < 2}\\{4x + 3}&{x \ge 2}\end{array}} \right.$ وارون‌پذیر است. حداقل مقدار k، کدام است؟
اگر تابع $f = \{ (1\,,\, - 2)\,,\,(a\,,\,2)\,,\,(b\,,\, - 2)\,,\,(1\,,\,{a^2} - 3a)\} $ یک به یک باشد، $a + b$ کدام است؟
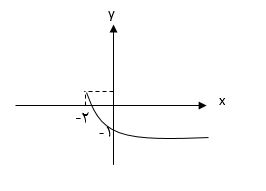
شکل مقابل نمودار تابع $f\left( x \right)=b-\sqrt{ax+b+۳}$ است. مقدار $f\left( ۳۰ \right)$ کدام است؟
