شرکت در آزمون آنلاین ریاضی هشتم - فصل ششم : مثلث

1- چه تعداد از اعداد \[{( - 1)^{1360}},101,61 + 71,231,1001\] اول هستند؟

هیچ

\[1\]

\[2\]

\[3\]

2- اندازة هر زاویۀ خارجی یک 36 ضلعی منتظم کدام گزینه است؟

\[90\]

\[10\]

\[17\]

\[36\]

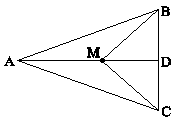
3- در شکل زیر \[\overline {AB} = \overline {BC} \] و \[\overline {AD} = \overline {DE} \] می‌باشد، کدام‌یک از تساوی‌های زیر نادرست است؟

\[\overline {AH} = \overline {NE} \]

\[\overline {MC} = \overline {NE} \]

\[\overline {HM} = \overline {BD} \]

\[\overline {HD} = \overline {DN} \]

4- در مثلث ABC ارتفاع BH را به اندازة AC و ارتفاع CH( را به اندازة AB امتداد می‌دهیم. نقاط به‌دست آمده را به رأس A وصل می‌کنیم، اگر \[{\hat A_1} + {\hat F_1} = 52\] باشد، اندازة زاویة \[{\hat A_1}\] برابر است با:

۲۰

۲۲

۲۴

۲۶

5- در شکل زیر، مثلث ABC متساوی‌الساقین و AD نیمساز زاویۀ A می‌باشد. کدام‌یک از تساوی‌های زیر نادرست است؟