شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل ششم : حد و پیوستگی
| آزمون شماره 345
کدام تابع در $x = 1$ حد ندارد، ولی مقدار دارد؟
اگر نمودار $f(x)$ به‌صورت مقابل باشد، حاصل $\mathop {\lim }\limits_{x \to {{( - 1)}^ + }} f(|x|) - \mathop {\lim }\limits_{x \to {{( - 3)}^ - }} f(|x + 2|)$ کدام است؟
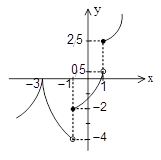
چه تعداد از گزاره‌های زیر صحیح است؟ الف) اگر تابع $f$ در a و تابع $g$ در $f(a)$ حد داشته باشند، $gof$ در a حد دارد. ب) اگر تابع $f$ در a و تابع g در $f(a)$ پیوسته باشند، gof در a پیوسته است. ج) اگر $(f + g)(x)$ و $(f - g)(x)$ در a پیوسته باشند، $f(x)$ و $g(x)$ در a پیوسته است.
تابع $f(x) = \left\{ \begin{array}{l}{x^2} - x\,\,\,\,\,\,\,\,x \ge k\\\frac{1}{x}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x < k\end{array} \right.$ مفروض است. به ازای کدام مقادیر k تابع $f(x)$ دقیقاً در دو نقطه ناپیوسته است؟
تابع f با ضابطه $f(x)=[x^{۲}]-[x]^{۲}$ در کدام نقطه زیر حد دارد ؟