شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل ششم : حد و پیوستگی
| آزمون شماره 955
تابع $f(x) = \left\{ \begin{array}{l}{x^2} - x\,\,\,\,\,\,\,\,x \ge k\\\frac{1}{x}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x < k\end{array} \right.$ مفروض است. به ازای کدام مقادیر k تابع $f(x)$ دقیقاً در دو نقطه ناپیوسته است؟
نمودار تابع $f$ به صورت مقابل است. کدام گزینه صحیح است؟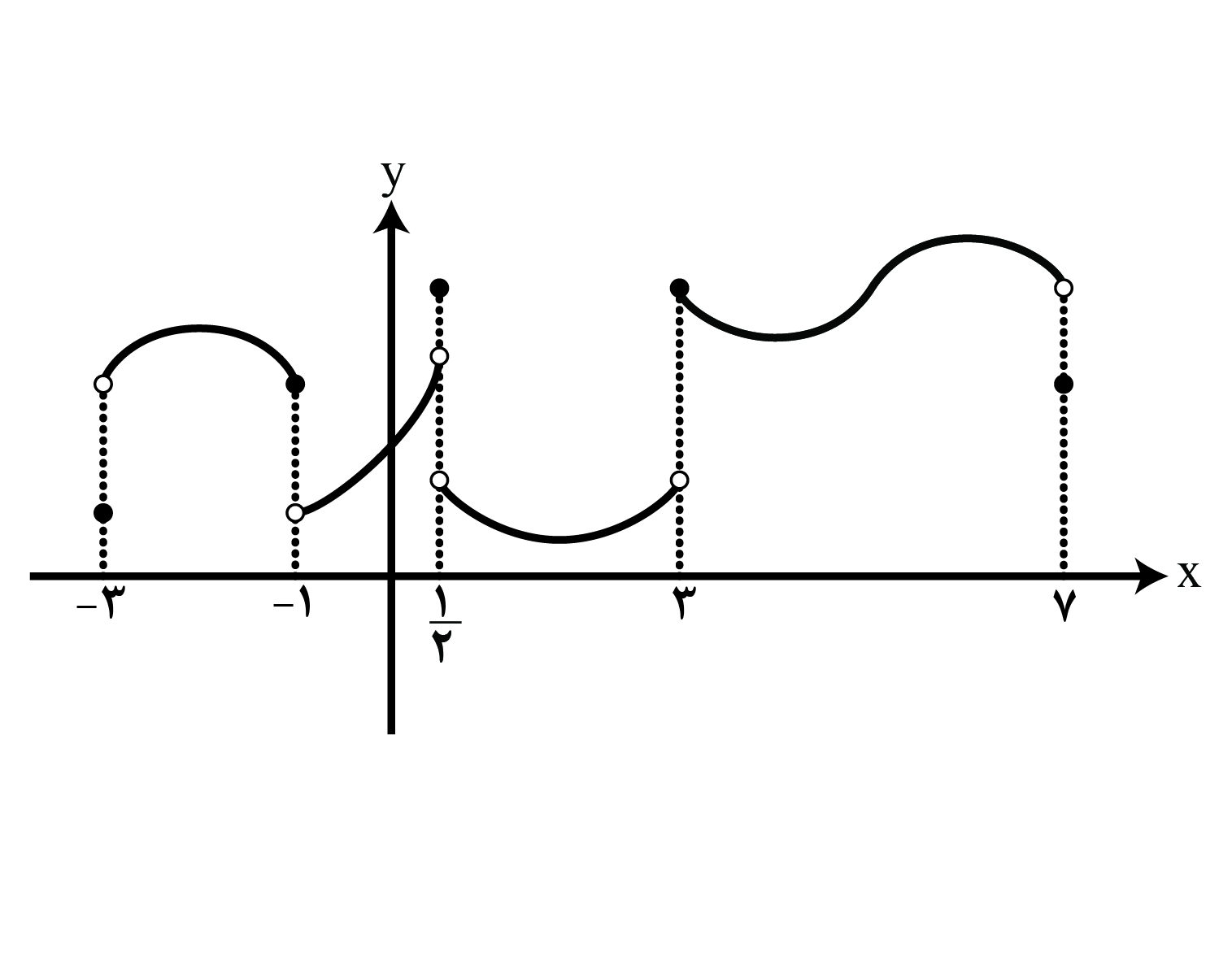
به ازای چند مقدار صحیح $\text{m}$، تابع $\text{f}\left( \text{x} \right)=\sqrt{{{\text{x}}^{۲}}+\text{mx}+۲}$ در هر نقطهای پیوسته است؟
