شرکت در آزمون آنلاین ریاضی 3 و پایه - فصل پنجم: کاربرد مشتق | آزمون شماره 396

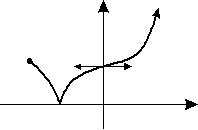
1- نمودار مقابل a تا اکسترمم نسبی، b تا اکسترمم مطلق و c تا نقطۀ بحرانی دارد. abc کدام است؟

2- در تابع \[y = {x^3} + 3{x^2} + ax - 4\]، اگر حاصل‌ضرب طول‌های نقاط اکسترمم نسبی تابع، برابر 1 باشد، a کدام است؟

3- مجموع طول‌های نقاط بحرانی تابع $f(x) = \left\{ {\begin{array}{*{20}{l}}{|x - 2| - 3}&{x > 0}\\{{x^2} + 2x - 1}&{ - 2 \le x \le 0}\end{array}} \right.$ کدام است؟

4-

 اگر $f\left( x \right)=\left| x-۳ \right|\sqrt{x}$ دربازه‌ی $\left[ ۰,۴ \right]$ تعریف شده باشد، اختلاف حداقل و حداکثر مقدار تابع کدام است؟

5-

مجموع مقادیر Max و min نسبی تابع $f(x)\,=\,\frac{۲{{x}^{۲}}}{x-۱}$ کدام است؟