شرکت در آزمون آنلاین
ریاضیات گسسته
-
درس 1: معرفی گراف
| آزمون شماره 137
حداقل چند یال دلخواه به گراف ناهمبند ۶-منتظم از مرتبه ۱۶ که دوبخش جدا ازهم آن هم مرتبه نیستند بیافزاییم تا مطمئن باشیم گراف حاصل همبند است؟
چند مقدار مختلف برای مرتبه گراف ساده ای وجود دارد که مجموع مرتبه واندازه آن $۱۰$ باشد؟
از بین گرافهای داده چند مورد آنها یک زیر برای گراف روبهرو نیستند؟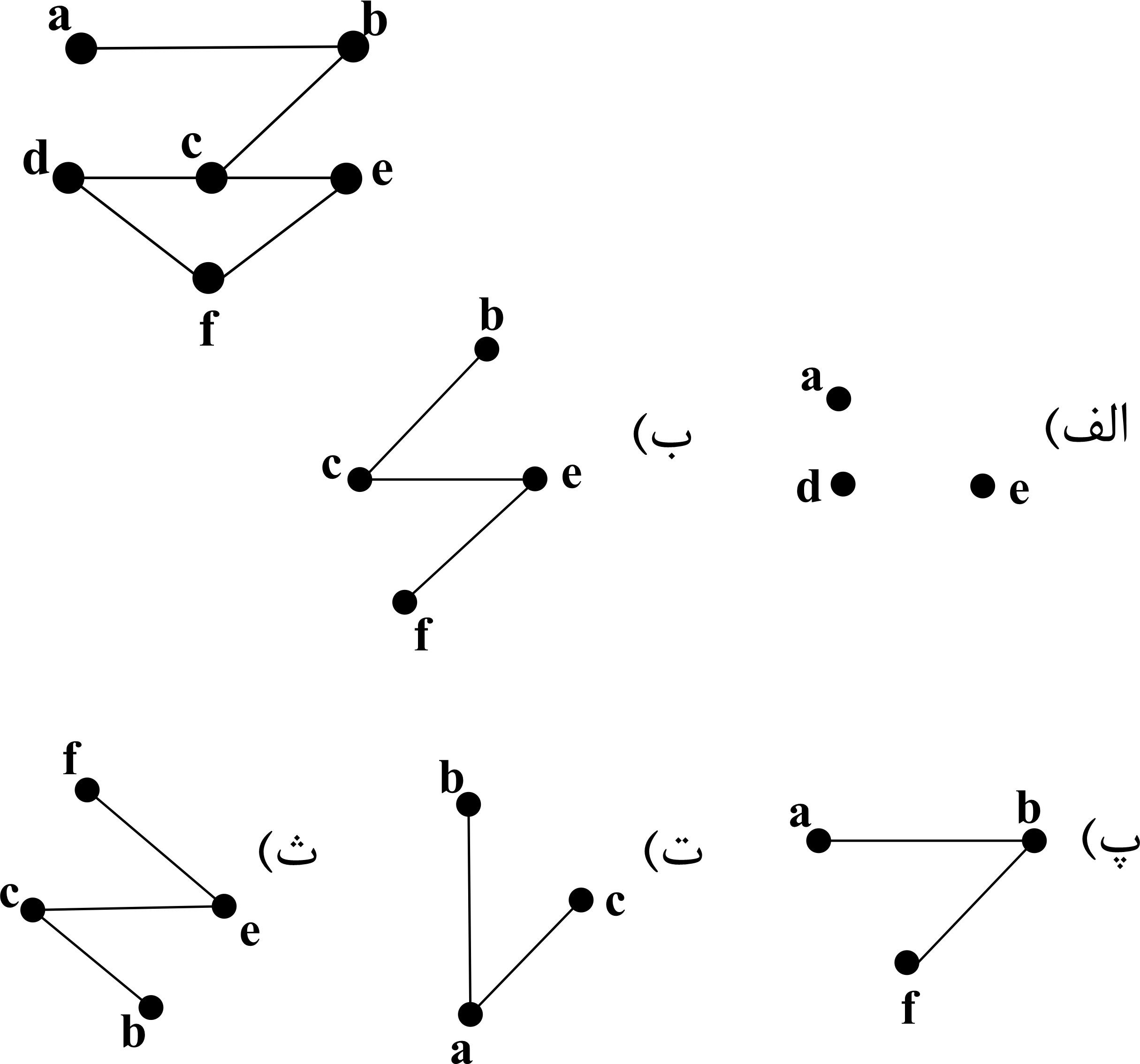
گراف $-k$منتظم $G$ از مرتبه ۱۷ ناهمبند است. $k$ چند مقدار متمایز میتواند باشد؟
در گراف $G$ با مجموعه رأسهای $\text{V}=\left\{ \text{a }\!\!~\!\!\text{ },\text{ }\!\!~\!\!\text{ b},\text{ }\!\!~\!\!\text{ c},\text{ }\!\!~\!\!\text{ d},\text{ }\!\!~\!\!\text{ e},\text{f} \right\}$ شرایط زیر برقرار است:
$\begin{cases} {{\text{N}}_{\text{G}}}\left( \text{d} \right)=\left\{ \text{b},\text{e,f} \right\}\\\!\text{ }\!\!~\!\!\text{ }{{\text{N}}_{\text{G}}}\left( \text{f} \right)=\left\{ \text{d} \right\}\\\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }{{\text{N}}_{\text{G}}}\left( \text{a} \right)=\left\{ \text{b},\text{c},\text{e} \right\}\\\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }{{\text{N}}_{\text{G}}}\left[ \text{b} \right]=\left\{ \text{b},\text{d},\text{a} \right\} \\\deg(e)=۲\\\deg(c)=۱\end{cases}$
کدام گزینه زیرگرافی از $G$ نیست؟
