شرکت در آزمون آنلاین
ریاضی نهم
-
فصل سوم: استدلال و اثبات در هندسه
| آزمون شماره 28055
در مثلث متساویالساقین ABC، نیمساز داخلی زاویة B و نیمساز خارجی زاویة C را رسم میکنیم، اندازة زاویة D چقدر است؟ \[(\overline {AB} = \overline {AC} ,\mathop A\limits^ \wedge = 2\mathop B\limits^ \wedge )\]
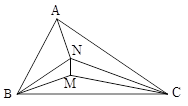
اگر N محل برخورد نیمسازهای داخلی مثلث ABC و M محل برخورد نیمسازهای داخلی BNC و \[B\hat MC = 150\] باشد، اندازة زاویة A کدام است؟
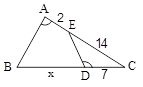
در شکل زیر \[\hat A = \hat D\]، طول BD کدام است؟ \[(\hat A = \hat D)\]
