شرکت در آزمون آنلاین هندسه 2 - فصل دوم : تبدیل های هندسی | آزمون شماره 822

1- رأس‌های \[A\]، \[B\] و \[C\] مثلث $A\mathop B\limits^\Delta  C$ را به مرکز محل تلاقی میانه‌های مثلث و با نسبت $K =  - \frac{1}{2}$ مجانس می‌کنیم و به ترتیب \[A'\]، \[B'\] و \[C'\] می‌نامیم. حاصل عبارت \[\frac{{A{{A'}^2} + B{{B'}^2} + C{{C'}^2}}}{{A{B^2} + A{C^2} + B{C^2}}}\] کدام است؟  

2- دو خط متقاطع d و \[d'\] دوران یافته یکدیگر به مرکز نقطة  Oو به زاویۀ \[{80^ \circ }\] می‌باشند. اگر محل تقاطع دو خط نقطة A باشد، زاویۀ OA با d کدام است؟

3-

دو پاره‌خط AB و CD در صفحه موازی یکدیگرند. مرکز تجانس آن‌ها کدام نقطه است؟

4- فرض کنید $M'$ مجانس نقطة M به مرکز O و نسبت $\frac{1}{4}$ باشد اگر $MM' = 12$ باشد، حاصل $O{M^2} + O{M'^2}$ کدام است؟

5-

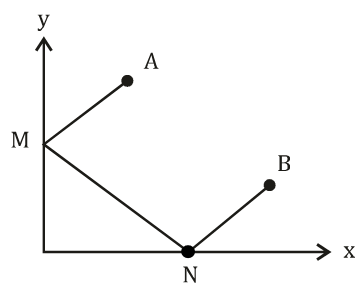
هرگاه دو دیوار میز بیلیارد را محورهای مختصات در نظر بگیریم. در صورتیکه مختصات توپ $A\left( ۱,۳ \right)$ و مختصات توپ $B\left( ۵,۱ \right)$  باشد، می‌خواهیم توپ B را به کمک توپ A و با برخورد با دو محور بزنیم. طول کوتاه‌ترین مسیر AMNB کدام است؟