شرکت در آزمون آنلاین هندسه 1 - فصل سوم: چند ضلعی ها | آزمون شماره 312

ABC مثلث متساوی‌الاضلاعی با مساحت $3\sqrt 3 $ است. اگر G مرکز ثقل یا محل همرسی میانه‌های مثلث ABC باشد، مجموع فواصل نقطة G از سه ضلع مثلث چقدر می‌شود؟

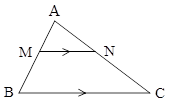
در شکل مقابل \[MN||BC\] و مساحت ذوزنقه 15 برابر مساحت مثلث AMN می‌باشد. حاصل \[\frac{{AC}}{{AN}}\] چقدر است؟

چهار نقطۀ $A\,(2\,,\,2)$ و $B\,(3\,,\,6)$ و $C\,(6\,,\,5)$ و $D\,(8\,,\,1)$ مفروض است. مساحت چهارضلعی ABCD کدام است؟

در مستطیل$ABCD$ شکل زیر$AB = 4$ و$BC = 6$ است. نقطه$M$ وسط ضلع$AB$ است و همچنین نقطه$N$ طوری روی ضلع$AD$ می‌کشیم که$AD = 2DN$ اندازۀ زاویۀ$N\widehat MC$ چقدر است؟

در چهارضلعی محدب ABCD دو قطر AC و BD بر هم عمودند. اگر اختلاف اندازه‌های دو قطر 6 سانتی‌متر باشد و مساحت چهارضلعی 360 سانتی‌مترمربع باشد، مجموع دو قطر چند سانتی‌متر است؟