شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل ششم : حد و پیوستگی
| آزمون شماره 336
1- تابع $f(x) = \left\{ {\begin{array}{*{20}{l}}{\sqrt[3]{{x - 1}}\,[x]}&{x \ge 2}\\{a{x^3} + b{x^2}}&{x < 2}\end{array}} \right.$ در $x = 2$ مشتقپذیر است. a کدام است؟
2- اگر $f(x) = \left\{ {\begin{array}{*{20}{l}}{\frac{{\sqrt {x + 1} - a}}{{x - 3}}}&{x > 3}\\{\frac{{\sqrt[3]{{x - 2}} - 3}}{{{x^2} + 1}} + b}&{x \le 3}\end{array}} \right.$ در $\mathbb{R}$ پیوسته باشد، b کدام است؟
3- اگر $f(x) = \left\{ \begin{array}{l}[x]\,\,\,\,\,\,\,x > - 1\\1 - [x]\,\,\,\,\,\,\,x \le - 1\end{array} \right.$، آنگاه حاصل $\mathop {\lim }\limits_{x \to 0} f({x^2} - 1)$ کدام است؟
4-
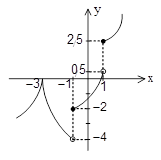
اگر نمودار $f(x)$ بهصورت مقابل باشد، حاصل $\mathop {\lim }\limits_{x \to {{( - 1)}^ + }} f(|x|) - \mathop {\lim }\limits_{x \to {{( - 3)}^ - }} f(|x + 2|)$ کدام است؟
5-
حاصل حد$\lim_{x\to-۲}(\frac{۳x^۲-x+۱۴}{x^۲-۴}+\frac{۳-۲x}{x+۲}) $ کدام است؟