شرکت در آزمون آنلاین
هندسه 2
-
فصل سوم : روابط طولی در شکل های هندسی
| آزمون شماره 1377
در مثلث قائم الزاویه $(A = {90^ \circ })\,ABC$ دو نقطۀ E و F را به ترتیب روی AB و AC به گونه‌ای انتخاب می‌کنیم که نیمسازهای زاویه‌های $E\hat FC$ و $F\hat EB$ یکدیگر را در نقطه P روی وتر قطع کنند. اگر $BP = 6$ و $CP = 8$ باشد حاصل $|AB - AC|$ چقدر است؟
در مثلث ABC با اضلاع $AB = 4$، $AC = 6$ و $BC = 8$، M وسط ضلع BC و MP و MQ نیمسازهای داخلی AMC و AMB هستند. در این صورت محیط مثلث APQ کدام است؟
طول های اضلاع یک مثلث، سه عدد طبیعی فرد متوالی هستند و زاویه روبرو به ضلع بزرگ مثلث $۱۲۰^{\circ}$ است. سینوس زاویه روبرو به کوچکترین ضلع، کدام است؟
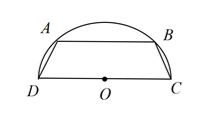
یک ذوزنقه متساوی الساقین به ساق ۲ داخل نیم دایره‌ای به شعاع ۴ محاط شده است. طول قاعده کوچک آن کدام است؟
