شرکت در آزمون آنلاین
هندسه 1
-
فصل دوم: تالس و تشابه
| آزمون شماره 5087
1- در مثلث قائم‌الزاوية ، از نقطة N وسط ضلع AC بر وتر BC عمود مي‌كنيم و پاي عمود را K مي‌ناميم و از K به وسط ضلع AB، نقطة M، وصل مي‌نماييم. مساحت چهارضلعي ANKM چه كسري از مساحت مثلث است؟
2- اگر $a = \frac{b}{2} = \frac{c}{3} = \frac{d}{{4 + b}}$ باشد، کمترین مقدار $a + b + c + d$ کدام است؟
3- در مثلث ، $BC\parallel ED$ و $EB\parallel DF$ است. اگر $AC = 4$ و $AF = 9$ باشد، $BE$ چه کسری از DF است؟
4-
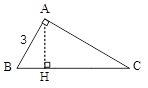
در مثلث قائم‌الزاویة $(A = 90^\circ )$، با رسم ارتفاع AH، نسبت مساحت‌های دو مثلث $\mathop {ABH}\limits^\Delta $ و \[\mathop {ACH}\limits^\Delta \] 1 به 4 می‌باشد. اگر $AB = 3$ باشد، طول وتر BC کدام است؟
5- در شکل مقابل\[MN||PB||CL\]و\[MP||BC\]می‌باشد. حاصل\[x + y\] کدام است؟ \[(PB = y{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} CP = x)\]