شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل سوم : توابع
| آزمون شماره 161
اگر دامنة تابع $f(x) = \frac{{{x^2} - \sqrt 3 x + 6}}{{3{x^2} - 12x + a}}$ به صورت ${D_f} = \mathbb{R} - \{ b\} $ باشد، مقدار $\frac{a}{b}$، کدام است؟
اگر \[f(x) = {x^2} - 2x - 8\] باشد، دامنة تابع \[g(x) = \sqrt[{}]{{\frac{{(x + 5)f(x)}}{{1 - x}}}}\] کدام است؟
در تابع f رابطة \[(x \ne 0)\,f(x) + 2\,f(\frac{{ - 1}}{x}) = 4x - 2\] برقرار است. \[f( - \frac{1}{2})\] کدام است؟
در تابع f رابطة \[(x \ne 0)\,f(x) + 2\,f(\frac{{ - 1}}{x}) = 4x - 2\] برقرار است. \[f( - \frac{1}{2})\] کدام است؟
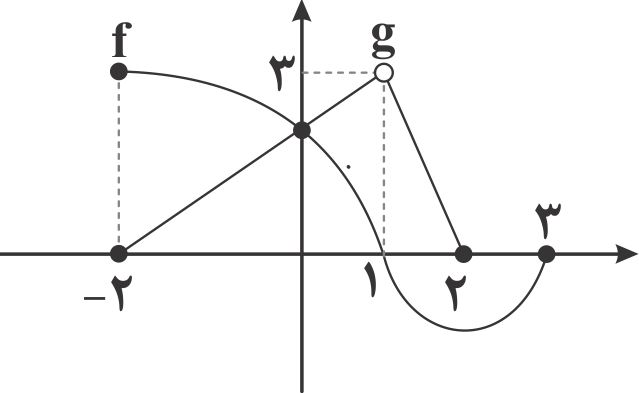
نمودار تابع های $f$ و $g$ مطابق شکل مقابل است. دامنه تابع $\frac{g}{f-g}$ کدام است؟
