 شرکت در آزمون آنلاین
ریاضی 3 و پایه
-
فصل سوم: حد
| آزمون شماره 63
شرکت در آزمون آنلاین
ریاضی 3 و پایه
-
فصل سوم: حد
| آزمون شماره 63
حاصل کدام حد موجود است؟
برای تابع پیوستۀ f میدانیم \[\mathop {\lim }\limits_{x \to 1} \frac{{f(x)}}{{{x^2} - 1}} = - \frac{1}{2}\] است. در این صورت \[\mathop {\lim }\limits_{h \to 0} \frac{{f(1 - 2h)}}{h}\] کدام است؟
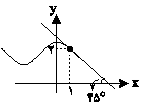
نمودار تابع \[y = f(x)\] و خط مماس بر آن رسم شده است. حاصل \[\mathop {\lim }\limits_{x \to 1} \frac{{f(x) - 2}}{{\sqrt x - 1}}\] کدام است؟
اگر $f(x) = \frac{{a\,|x - 2|}}{{3x - \sqrt {{x^2} + 32} }}$ و \[\mathop {\lim }\limits_{x \to {2^ - }} f(x) = \frac{{ - 1}}{4}\] باشد، حاصل $\mathop {\lim }\limits_{x \to - \infty } f(x)$ کدام است؟
اگر \[\mathop {\lim }\limits_{x \to - \,\infty } \frac{{a{x^n} - \sqrt[{}]{{9{x^2} - 6x + 2}}}}{{3x - |2x + 5|}} = - 1\] باشد، حاصل \[\mathop {\lim }\limits_{x \to + \,\infty } \frac{{(a + 6)\sqrt[{}]{x}}}{{\sqrt[{}]{{4x + 1}} - 1}}\] کدام است؟


