شرکت در آزمون آنلاین
ریاضی 3 و پایه
-
فصل پنجم: کاربرد مشتق
| آزمون شماره 504
1-
یک پنجرۀ بزرگ با محیط 30 متر به شکل یک نیم‌دایره و یک مستطیل ساخته شده است. به‌ازای چه مقداری از x، این پنجره بیشترین نوردهی را دارد؟
2- چه تعداد از گزاره‌های زیر صحیح هستند؟ الف) اگر نقطة $x = c$ یک نقطة اکسترمم مطلق تابع f باشد، آنگاه $x = c$ نقطة اکسترمم نسبی تابع f نیز خواهد بود. ب) اگر در نقطة $x = c$، $f'(c)$ موجود و مخالف صفر باشد، آنگاه نقطة $x = c$ نمی‌تواند نقطة اکسترمم نسبی تابع f باشد. ج) اگر تابع f در بازة $(a\,,\,b)$ تابعی صعودی یا تابعی نزولی باشد، آنگاه در این بازه، قطعاً فاقد اکسترمم نسبی خواهد بود.
3- اگر نقطۀ $A(a\,,\,b)$ نقطۀ ماکزیمم مطلق تابع $f(x) = 2{x^5} - 2{x^4} - 6{x^3} + 8$ روی بازۀ $[ - 2\,,\,1]$ باشد، مقدار ab کدام است؟
4-
نمودار تابع $f\left( x \right)=\frac{ax}{{{x}^{۲}}+b}$ به صورت مقابل است. مقدار $a+b$ کدام است؟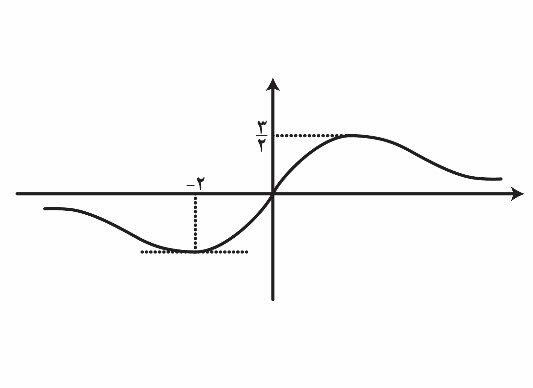
5-
در بین تمام مثلث‌های قائم الزاویه با مساحت واحد، کم‌ترین مقدار وتر کدام است؟