شرکت در آزمون آنلاین
هندسه 3
-
فصل دوم : مقاطع مخروطی
| آزمون شماره 279
در شکل زیر F، S و d به ترتیب کانون، رأس و خط هادی سهمی هستند. اگر کوتاهترین فاصلۀ نقاط سهمی از خط هادی برابر \[\frac{5}{2}\] باشد، طول MN چقدر است؟
در شکل مقابل نقطه M روی بیضی و کانون های $F$ و ${F}'$ مشخص شده اند . خط d را به گونه ای رسم میکنیم که در نقطه M بر بیضی مماس باشد و سپس از نقطه ${F}'$ خطی موازی با MF رسم میکنیم تا خط d را در نقطه ای مانند N قطع کند. اگر قطر بزرگ بیضی ۱۰ و $N{F}'-MF=۴$ باشد، اندازه $M{F}'$ چقدر است؟
معادله خط هادی یک سهمی $x=-۱$ است. یک منبع نورانی از نقطهای به مختصات $(۳,۲)$ قرار گرفته و بازتاب هر پرتو آن پس از برخورد به سهمی، به موازات محور x ها میباشد. این سهمی محور x هارا در کدام نقطه قطع میکند؟
در سهمی ${{x}^{۲}}=۴y$، خط $y=x+۲$ سهمی را در دو نقطۀ $P$ و $Q$ قطع میکند، اگر کانون سهمی نقطه F باشد، حاصل $QF+PF$ کدام است؟
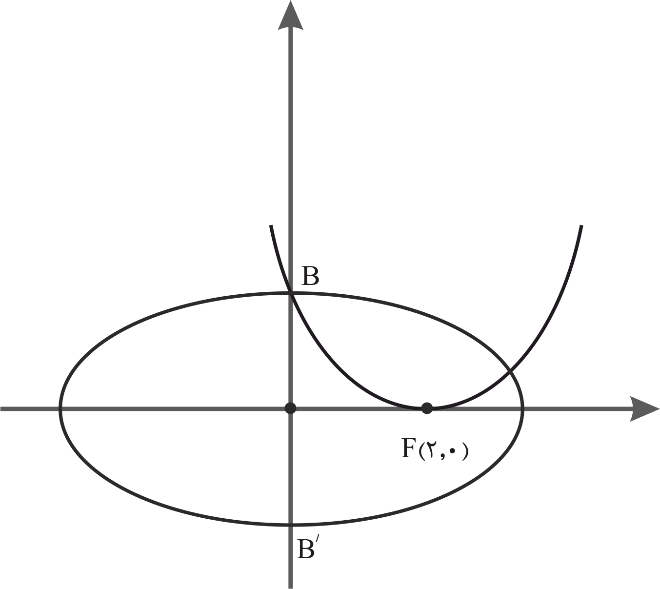
در شکل مقابل، راس سهمی بر کانون بیضی منطبق بوده و سهمی از رأس ناکانونی بیضی میگذرد. اگر $e=\frac{۲}{\sqrt{۵}}$ (خروج از مرکز بیضی) باشد. فاصله کانون تا رأس سهمی چقدر است؟
