شرکت در آزمون آنلاین ریاضی 3 و پایه - فصل چهارم: مشتق

اگر $f''(x) = \sqrt[3]{x}$ باشد، در این صورت مشتق تابع f روی کدام بازه اکیداً صعودی است؟

$[۰\,,\, + \infty )$

$( - \infty \,,\,۰]$

$\mathbb{R}$

نمی‌توان تعیین کرد.

کدام تابع در $x = 0$ دارای مماس قائم نیست؟

$y = \sqrt[۳]{{{x^۲}}}$

$y = \sqrt[۳]{x}$

$y = x\sqrt[۳]{x}$

$y = \sqrt[۳]{{|x|}}$

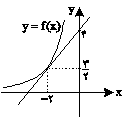
اگر خط مماس بر نمودار تابع f در نقطة $x = - 2$ به صورت مقابل باشد، حاصل $\mathop {\lim }\limits_{h \to 0} \frac{{f( - 2) - f( - 2 - h)}}{{2h}}$ کدام است؟

$- \frac{۵}{۸}$

$\frac{۵}{۸}$

$\frac{۵}{۴}$

$- \frac{۵}{۴}$

4-

اگر $~f\left( x \right)=\frac{۸{{x}^{۳}}-۱۲{{x}^{۲}}+۶x-۱}{۱۲{{x}^{۲}}+۱۰x}$ باشد، مقدار مشتق تابع $y=\sqrt[۳]{f\left( x \right)}$ در $x=\frac{۱}{۲}$ کدام است؟

۱

۲

۳

۴

5-

اگر $f\left( x \right)=\left\{ \begin{align} & {{x}^{۲}}+۲x\,\,\,\,\,\,\,\,\,x\geq ۲ \\ & {{x}^{۳}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x<۲ \\ \end{align} \right.$ باشد، مقدار $\underset{h\to {{۰}^{-}}}{\mathop{lim}}\,\frac{f\left( ۲-۲h \right)-f\left( ۲ \right)}{h}$ کدام است؟

$۱۲$

$-۱۲$

$۲۴$

$-۲۴$

شرکت در آزمون آنلاین ریاضی 3 و پایه - فصل چهارم: مشتق | آزمون شماره 99

جست و جو

شرکت در آزمون آنلاین ریاضی 3 و پایه - فصل چهارم: مشتق | آزمون شماره 99

جست و جو

ساخت آزمون

ساخت آزمون