شرکت در آزمون آنلاین
هندسه 2
-
فصل سوم : روابط طولی در شکل های هندسی
| آزمون شماره 125
شرکت در آزمون آنلاین
هندسه 2
-
فصل سوم : روابط طولی در شکل های هندسی
| آزمون شماره 125
مثلث ABC به طول اضلاع 5، 10و 12 را در نظر بگیرید. نیمسازهای داخلی و خارجی بزرگترین زاویه داخلی مثلث را رسم میکنیم تا ضلع دیگر و امتداد آن را به ترتیب در D و \[D'\] قطع کنند. نسبت مساحت کوچکترین مثلث به مساحت بزرگترین مثلث ایجاد شده چقدر است؟
در مثلث ABC طول اضلاع ۱۳ و ۱۴ و ۱۵ واحد است.
نقطه M به فاصله ۵ واحد از کوچکترین ضلع و ۵ واحد از بزرگترین ضلع این مثلث قرار دارد. فاصله M از ضلع متوسط کدام است؟
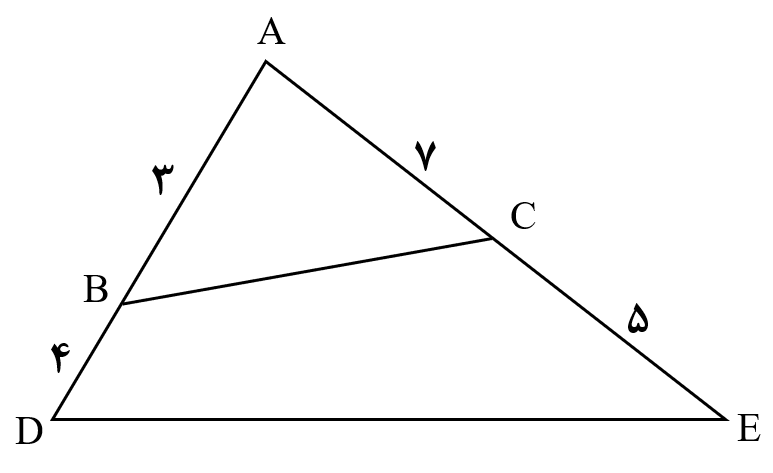
در شکل مقابل مساحت چهار ضلعی BCED چند برابر مساحت مثلث ADE است؟

در مثلث ABC داریم: $P-a=۴$ و $P-b=۵$ و $P-c=۶$. مساحت مثلث کدام است؟
(P نصف محیط مثلث است)
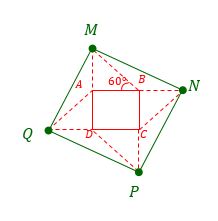
روی اضلاع مربع $ABCD$، چهار مثلث قائمالزاویه همنهشت با یک زاویۀ °۶۰ بنا کردهایم. مساحت چهارضلعی $MNPQ$ چند برابر مساحت چهار ضلعی $ABCD$ است؟