شرکت در آزمون آنلاین هندسه 2 - فصل دوم : تبدیل های هندسی

1- زمینی مطابق شکل مفروض است. می‌خواهیم به کمک تبدیل‌های هندسی مساحت آن را افزایش دهیم، به طوری‌که محیط آن تغییر نکند. اگر مساحت افزایش یافته برابر 24 باشد، مقدار x کدام است؟

۴

۳

۲

۱

مثلث قائم‌الزاویة متساوی‌الساقین $(\mathop A\limits^ \wedge = {90^ \circ })\mathop {ABC}\limits^\Delta$ مفروض است. نقطة M واقع در وسط AB را نسبت به ضلع AC بازتاب می‌کنیم و سپس تصویر آن را نسبت به ضلع BC بازتاب می‌کنیم و $M'$ می‌نامیم. طول $MM'$ چند برابر طول وتر مثلث $\mathop {ABC}\limits^\Delta$ است؟

$1$

$\frac{{\sqrt 2 }}{2}$

$\frac{{\sqrt 3 }}{2}$

$\frac{{\sqrt 5 }}{2}$

خطوط $L:2x + y = 1$ و $d:x - 2y = 3$ مفروض‌اند. بازتاب خط L را نسبت به d به‌دست می‌آوریم و آن را $L'$ می‌نامیم. اگر فاصلة نقطة $A\,(a,b)$ روی خط $L'$ از خط d برابر $3\sqrt[{}]{5}$ باشد، $a + b$ کدام است؟

۴

$- ۴$

۳

$- ۳$

4-

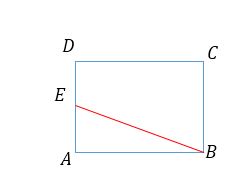
مستطیل $ABCD$ به اضلاع ۳ و ۵ مفروض است( $AD=۳$ ). اگر تصویر $A$ دربازتاب نسبت به محور $BE$ روی ضلع $CD$ قرار گیرد؛ نقطه $E$ ضلع $AD$ به چه نسبتی تقسیم می‌کند؟