شرکت در آزمون آنلاین هندسه 1 - فصل اول: ترسیم های هندسی و استدلال

در مثلث ABC نقطۀ M روی ضلع BC قرار دارد. اگر \[M\hat AC = {32^ \circ }\] ، \[\hat B = {47^ \circ }\] و \[\hat C = {36^ \circ }\] آنگاه چند تا از نامساوی‌های زیر درست است؟ الف) \[AC > AB\] ب) \[BM > AB\] ج) \[BM > AM\] د) \[AC > AM\]

\[1\]

\[2\]

\[3\]

\[4\]

مثلث $\mathop {ABC}\limits^\Delta $ با معلوم بودن $b = 16$ و$c = 4$و${m_a}$ قابل رسم است. ${m_a}$ کدام عدد می‌تواند باشد؟

۱۰

۱۱

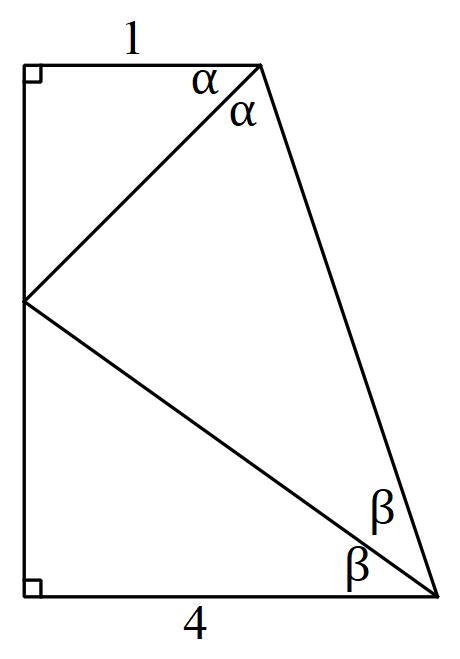
با توجه به شکل مقابل مساحت ذوزنقه کدام است؟

۱۰

۱۰/۵

۱۲

۱۲/۵

در مثلث متساوی الساقین $\text{ABC }\!\!~\!\!\text{ }$از نقطه ی اختیاری $\text{D}$ واقع بر قاعده $\text{BC }\!\!~\!\!\text{ }$، عمود $\text{DH}$ را بر ساق $\text{AC}$ وارد میکنیم. زاویه $\text{A}$ چند برابر زاویه $\text{HDC}$ است؟