شرکت در آزمون آنلاین
ریاضی 3 و پایه
-
فصل پنجم: کاربرد مشتق
| آزمون شماره 147
1- دامنۀ تابع $f(x) = 4{x^3} - 8{x^2} + 3$ بازۀ $[ - \frac{1}{2}\,,\,3]$ و برد آن بازۀ $[a\,,\,b]$ است. تعداد اعداد صحیح در بازۀ $[a\,,\,b]$ کدام است؟
2-
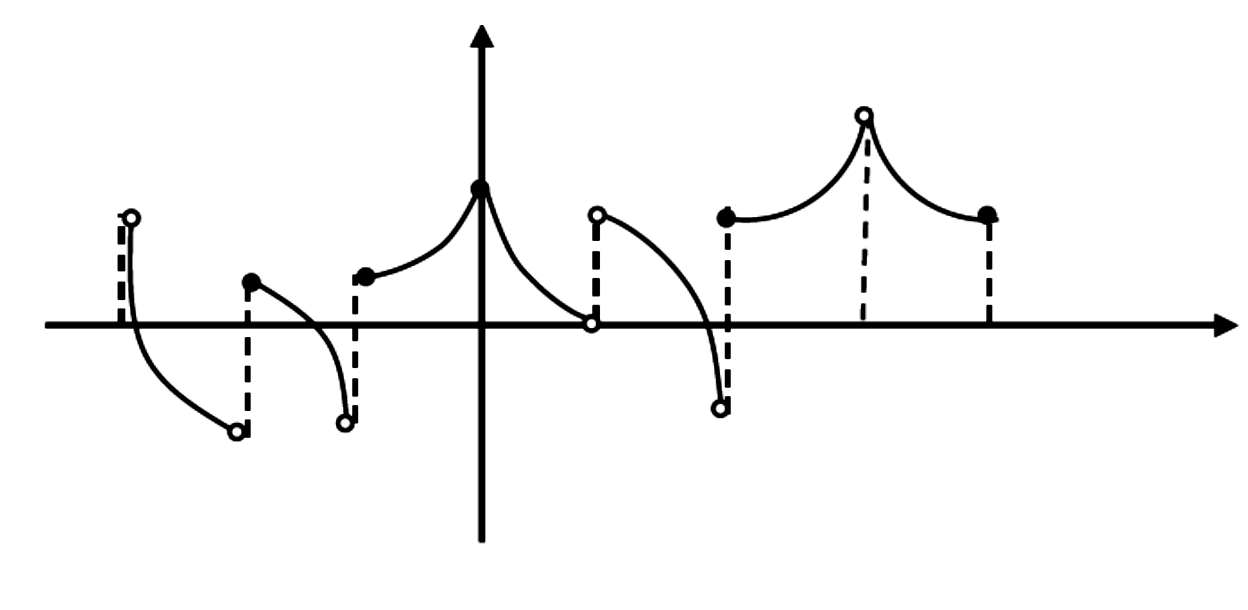
اگر شکل مقابل نمودار تابع $y=f(x)$ باشد، تعداد نقاط اکسترمم های نسبی تابع f کدام است؟
3- اگر $(3\,,\,9)$ ماکزیمم نسبی تابع $f(x) = x\sqrt {ax + b} $ باشد، b کدام است؟
4- تابع \[f(x) = \frac{{|x|\, + \,| - x|}}{{[x] + [ - x]}}\] به ترتیب دارای چند نقطة بحرانی و چند نقطة اکسترمم نسبی است؟
5- در تابع با ضابطۀ $f(x) = x|x + 2|$، فاصلۀ نقاط ماکزیمم و مینیمم نسبی تابع کدام است؟