شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل سوم : توابع
| آزمون شماره 202
اگر \[f(x) = \frac{{2{x^2} + x + (1 - a)\sqrt[{}]{x}}}{{ax + 5}}\] یک تابع گویا باشد، \[f(1)\] چقدر است؟
نمودار تابع $f(x) = \sqrt {4 - 2x} $ را ابتدا یک واحد به سمت چپ و سپس دو واحد به پایین منتقل کرده و در نهایت نسبت به محور yها قرینه می‌کنیم. نمودار جدید محور xها را در نقطه‌ای با طول $\alpha $ قطع می‌کند. $\alpha $ کدام است؟
وارون تابع با ضابطة $y = 6 - \sqrt {2x - 1} $ کدام است؟
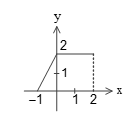
نمودار تابع $y = f(x - 1)$ به‌صورت مقابل است. نمودار تابع $y = f(x + 2) + 1$ کدام است؟
/
اگر $\text{f}=\left\{ \left( ۲,-۱ \right),\left( ۳,۵ \right),\left( -۱,۴ \right) \right\}$ و $\text{g}=\left\{ \left( a,۲b-۱ \right),\left( ۲,۵ \right),\left( ۴,۲ \right) \right\}$ و $۲\text{f}+\text{g}=\left\{ \left( ۲,۳ \right),\left( ۳,۱۱ \right) \right\}$ مقدار $\text{a}-\text{b}$ کدام است؟