شرکت در آزمون آنلاین
ریاضی 3 و پایه
-
فصل پنجم: کاربرد مشتق
| آزمون شماره 144
در تابع با ضابطۀ $f(x) = x|x + 2|$، فاصلۀ نقاط ماکزیمم و مینیمم نسبی تابع کدام است؟
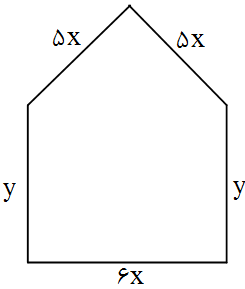
محیط شکل مقابل برابر $۳۶$ واحد است. اگر مساحت آن بیشترین باشد، مقدار $y$ کدام است؟
طول $Min$ نسبی تابع $f\left( x \right)=m{{x}^{۳}}+\left( ۹-{{m}^{۲}} \right)x+۴$ کوچک‌تر از طول $Max$ نسبی آن است. حدود $m$ کدام است؟
نمودار تابع $y={{x}^{۳}}-۶{{x}^{۲}}+۹x$ کدام است؟
فاصله نقاط ماکزیمم و مینیمم نسبی تابع با ضابطه $\text{f}\left( \text{x} \right)=\text{x}\sqrt{۲-{{\text{x}}^{۲}}}$ کدام است؟
