شرکت در آزمون آنلاین
ریاضی 2 (رشته تجربی)
-
فصل سوم : توابع
| آزمون شماره 330
اگر وارون تابع $f(x) = 3{x^2} + 6x + 2$ با دامنة $( - \infty \,,\, - 1]$ به صورت ${f^{ - 1}}(x) = a - \sqrt {\frac{{x + 1}}{b}} $ باشد، حاصل $a + b$ کدام است؟
اگر $f(x) = \sqrt {4 - {x^2}} $ باشد، دامنۀ تابع $f(1 - 2x)$ کدام است؟
اگر \[f(x) = \frac{{2{x^2} + x + (1 - a)\sqrt[{}]{x}}}{{ax + 5}}\] یک تابع گویا باشد، \[f(1)\] چقدر است؟
نمودار تابع با ضابطۀ $f(x) = \sqrt x $ را در امتداد محور xها، 11 واحد در جهت منفی و سپس در امتداد محور yها، 3 واحد در جهت منفی انتقال می‌دهیم. فاصلۀ نقطۀ برخورد منحنی حاصل با نمودار تابع f، از مبدأ مختصات کدام است؟
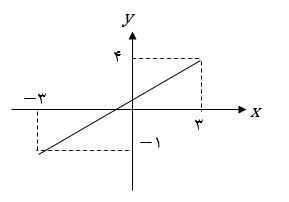
نمودار تابع $y=f\left( x \right)$ به صورت زیر است. کدام نمودار تابع $y=\left| x \right|$ را در نقاط بیشتری قطع می‌کند؟
