شرکت در آزمون آنلاین
هندسه 2
-
فصل سوم : روابط طولی در شکل های هندسی
| آزمون شماره 211
در مثلث قائم‌الزاویه \[(\mathop A\limits^ \wedge = {90^ \circ })ABC\] به اضلاع قائم 6 و 8 واحد، نیمساز زاویۀ C (کوچک‌ترین زاویۀ داخلی مثلث)، نیمساز بزرگ‌ترین زاویۀ داخلی مثلث را در نقطۀ O قطع می‌کند. نسبت مساحت دو مثلثی که در طرفین OC ایجاد می‌شود و OC یکی از اضلاع آنها است، چقدر است؟
در شکل زیر مساحت چهارضلعی \[ABCD\] کدام است ؟
در شکل مقابل AD نیمساز می‌باشد. اندازة ضلع AC کدام است؟
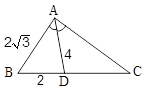
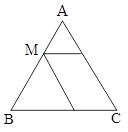
در شکل مقابل \[AM = \frac{1}{3}MB\] و چهارضلعی متوازی‌الاضلاع می‌باشد، مساحت متوازی‌الاضلاع چند درصد مساحت مثلث ABC است؟
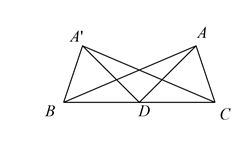
در شکل زیر $AD$ نیمساز $B\hat{A}C $ و ${A}'D$ نیمساز $B\hat{{A}'}C$ است. کدام گزینه صحیح است؟
