شرکت در آزمون آنلاین
ریاضی 3 و پایه
-
فصل چهارم: مشتق
| آزمون شماره 32
1- تابع $f(x) = \left\{ {\begin{array}{*{20}{c}}{|{x^2} - x|}&{}&{x < 1}\\{{x^2} + ax + b}&{}&{x \ge 1}\end{array}} \right.$ در $x = 1$ مشتق‌پذیر است. حاصل $a + 2b$ کدام است؟
2-
حاصل $\mathop \lim_{x \to ۱} {( x^۳-x+۱)(x^۲+x+۱)-۳ \over x^۳-۱}$ کدام است؟
3-
آهنگ متوسط تغییر تابع $f(x)=x^۲+۳ x+۳$ وقتی که از $x_۱ $ به اندازه h تغییر کند، کدام است؟
4-
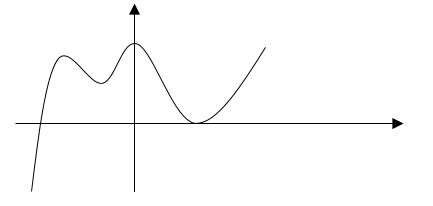
در چند نقطه مثل a روی نمودار تابع مقابل داریم $f(a)=f'(a)=۰$ ؟
5-
اگر تابع با ضابطه‌ی $f~\left( x \right)=\left\{ \begin{matrix} \frac{a}{x-۲}~~~~~~~~~~~~x>۴ \\ b\sqrt{x}+۱~~~~~x\le ۴ \\ \end{matrix} \right.$ در تمام نقاط مثبت مشتق پذیر باشد، حاصل $a-b$ کدام است؟